Back to all Sections from polar moment of inertia
Calculate polar moment of inertia
Section 16
Polar moment of inertia
It is called the moment of inertia of a system of material points in relation to a plane, an axis or a pole, the sum of the products between the masses of the particles that make up the system and the square of the distances of these particles to the plane, axis or pole considered:
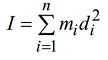
Compared to a Cartesian reference system we have:
- polar moments of inertia:
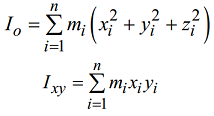
The polar moment of inertia can be calculated as:
- the semisum of the axial moments of inertia in relation to three rectangular axes passing through that point:
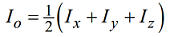
- the sum of planar moments of inertia:
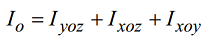
- the sum of the moments of inertia in relation to a plane and a normal axis to that plane:
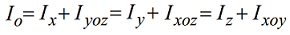
Id = Polar moment of inertia (cm4)
Wd = Torsional strength module (cm3)
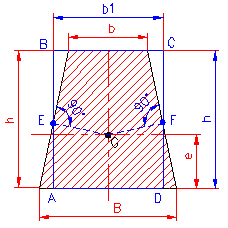
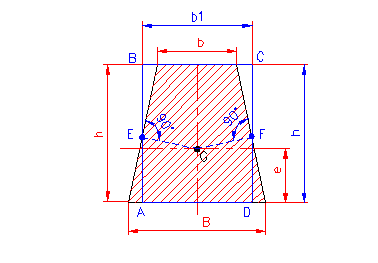
The surface of the trapezoid is assimilated with a rectangle ABCD (blue) of the same height (h), which is constructed as follows:
1. Determine the dimension (e) of the center of gravity (G) of the formula:
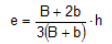
2. Determine the base (b1) of the assimilated rectangle:
– from the center of gravity (G) it descends perpendicularly on the sides and points (E) and (F) are obtained from which it descends perpendicularly on the base (D) of the trapezoid in points (A) and (D).
3. Thus is obtained the assimilated rectangle ABCD with base (b1) and height (h) which are denoted to be used as follows:
– choose Section 10 in which the dimensions of the rectangle ABCD (b1 and h) are entered and thus Id and Wd are determined for the given trapezoid.
Suggestion for polar moment of inertia. Send us your suggestion to improve this chapter.
